Vanishing and Exploding Gradient Problem
Deep neural networks have several stability issues associated with training. In particular, networks with many layers may be hard to train because of the way in which the gradients in earlier and later layers are related.In order to understand this point, let us consider a very deep network that has a single node in each layer. We assume that there are $(m + 1$) layers, including the non computational input layer. The weights of the edges between the various layers are denoted by $w_1, w_2, . . . w_m$. Furthermore, assume that the sigmoid activation function $\Phi(·)$ is applied in each layer. Let $x$ be the input, $h_1 . . . h_{m−1}$ be the hidden values in the various layers, and $o$ be the final output. Let ${Φ}'(h_t)$ be the derivative of the activation function in hidden layer $t$. Let $\frac{∂L}{∂h_t}$ be the derivative of the loss function with respect to the hidden activation $h_t$. The neural architecture is illustrated in Figure below
It is relatively easy to use the backpropagation update to show the following relationship:$\frac{∂L}{∂h_t}= {Φ}'(h_{t+1}) · w_{t+1}· \frac{∂L}{∂h_{t+1}}$
Since the fan-in is 1 of each node, assume that the weights are initialized from a standard normal distribution. Therefore, each wt has an expected average magnitude of 1.
Let us examine the specific behavior of this recurrence in the case where the sigmoid activation is used. The derivative with a sigmoid with output $f ∈ (0, 1)$ is given by $f(1−f)$.This value takes on its maximum at $f = 0.5$, and therefore the value of ${Φ}'(h_t)$ is no more than 0.25 even at its maximum. Since the absolute value of $w_{t+1}$ is expected to be 1, it follows that each weight update will (typically) cause the value of $\frac{∂L}{∂ht}$ to be less than 0.25 that of $\frac{∂L}{∂h_{t+1}}$. Therefore, after moving by about $r$ layers, this value will typically be less than $0.25r$. Just to get an idea of the magnitude of this drop, if we set $r = 10$, then the gradient update magnitudes drop to $10^{−6}$ of their original values! Therefore, when backpropagation is used, the earlier layers will receive very small updates compared to the later layers. This problem is referred to as the vanishing gradient problem.
Note that we could try to solve this problem by using an activation function with larger gradients and also initializing the weights to be larger. However, if we go too far in doing this, it is easy to end up in the opposite situation where the gradient explodes in the backward direction instead of vanishing. In general, unless we initialize the weight of every edge so that the product of the weight and the derivative of each activation is exactly 1, there will be considerable instability in the magnitudes of the partial derivatives. In practice, this is impossible with most activation functions because the derivative of an activation function will vary from iteration to iteration.
Although we have used an oversimplified example here with only one node in each layer, it is easy to generalize the argument to cases in which multiple nodes are available in each layer. In general, it is possible to show that the layer-to-layer backpropagation update includes a matrix multiplication (rather than a scalar multiplication). Just as repeated scalar multiplication is inherently unstable, so is repeated matrix multiplication. In particular, the loss derivatives in layer-$(i + 1)$ are multiplied by a matrix referred to as the Jacobian . The Jacobian contains the derivatives of the activations in layer-$(i+1)$ with respect to those in layer $i$. In certain cases like recurrent neural networks, the Jacobian is a square matrix and one can actually impose stability conditions with respect to the largest eigenvalue of the Jacobian. These stability conditions are rarely satisfied exactly, and therefore the model has an inherent tendency to exhibit the vanishing and exploding gradient problems. Furthermore, the effect of activation functions like the sigmoid tends to encourage the vanishing gradient problem. One can summarize this problem as follows:
The relative magnitudes of the partial derivatives with respect to the parameters in different parts of the network tend to be very different, which creates problems for gradient-descent methods.
Geometric Understanding of the Effect of Gradient Ratios
The vanishing and exploding gradient problems are inherent to multivariable optimization, even in cases where there are no local optima. In fact, minor manifestations of this problem are encountered in almost any convex optimization problem. Consider the simplest possible case of a convex, quadratic objective function with a bowl like shape and a single global minimum. In a single-variable problem, the path of steepest descent (which is the only path of descent), will always pass through the minimum point of the bowl (i.e., optimum objective function value). However, the moment we increase the number of variables in the optimization problem from 1 to 2, this is no longer the case. The key point to understand is that with very few exceptions, the path of steepest descent in most loss functions is only an instantaneous direction of best movement, and is not the correct direction of descent in the longer term. In other words, small steps with “course corrections” are always needed. When an optimization problem exhibits the vanishing gradient problem, it means that the only way to reach the optimum with steepest-descent updates is by using an extremely large number of tiny updates and course corrections, which is obviously very inefficient.
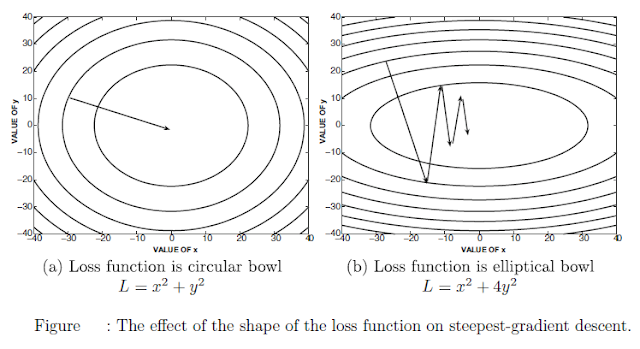
In order to understand this point, lets look at two bivariate loss functions in Figure . In this figure, the contour plots of the loss function are shown, in which each line corresponds to points in the XY-plane where the loss function has the same value. The direction of steepest descent is always perpendicular to this line. The first loss function is of the form $L = x^2 + y^2$, which takes the shape of a perfectly circular bowl, if one were to view the height as the objective function value. This loss function treats $x$ and $y$ in a symmetric way.The second loss function is of the form $L = x^2 +4y^2$, which is an elliptical bowl. Note that this loss function is more sensitive to changes in the value of $y$ as compared to changes in the value of $x$, although the specific sensitivity depends on the position of the data point.
In the case of the circular bowl of Figure (a), the gradient points directly at the optimum solution, and one can reach the optimum in a single step, as long as the correct step-size is used. This is not quite the case in the loss function of Figure (b), in which the gradients are often more significant in the $y$-direction compared to the $x$-direction.Furthermore, the gradient never points to the optimal solution, as a result of which many course corrections are needed over the descent. A salient observation is that the steps along the $y$-direction are large, but subsequent steps undo the effect of previous steps. On the other hand, the progress along the $x$-direction is consistent but tiny. Although the situation of highly unstable in terms of the sensitivity of the output to the parameters in different parts of the network. The problem of differing relative derivatives is extraordinarily large in real neural networks, in which we have millions of parameters and gradient ratios that vary by orders of magnitude. Furthermore, many activation functions have small derivatives, which tends to encourage the vanishing gradient problem during backpropagation. As a result, the parameters in later layers with large descent components are often oscillating with large updates, whereas those in earlier layers make tiny but consistent updates. Therefore, neither the earlier nor the later layers make much progress in getting closer to the optimal solution.As a result, it is possible to get into situations where very little progress is made even after training for a long time.
Partial Fix with Activation Function Choice
The specific choice of activation function often has a considerable effect on the severity of the vanishing gradient problem. The derivatives of the sigmoid and the tanh activation functions are illustrated in Figure $(a)$ and $(b)$ below , respectively. The sigmoid activation function never has a gradient of more than 0.25, and therefore it is very prone to the vanishing gradient problem. Furthermore, it saturates at large absolute values of the argument, which refers to the fact that the gradient is almost 0. In such cases, the weights of the neuron change very slowly.
Therefore, a few such activations within the network can significantly affect the gradient computations. The tanh function fares better than the sigmoid function because it has a gradient of 1 near the origin, but the gradient saturates rapidly at increasingly large absolute values of the argument. Therefore, the tanh function will also be susceptible to the vanishing gradient problem.
In recent years, the use of the sigmoid and the tanh activation functions has been increasingly replaced with the ReLU and the hard tanh functions. The ReLU is also faster to train because its gradient is efficient to compute. The derivatives of the ReLU and the hard tanh functions are shown in Figure (c) and (d), respectively. It is evident that these functions take on the derivative of 1 in certain intervals, although they might have zero gradient in others. As a result, the vanishing gradient problem tends to occur less often, as long as most of these units operate within the intervals where the gradient is 1.In recent years, these piecewise linear variants have become far more popular than their smooth counterparts. Note that the replacement of the activation function is only a partial fix because the matrix multiplication across layers still causes a certain level of instability.Furthermore, the piecewise linear activations introduce the new problem of dead neurons.
Dying Neurons and “Brain Damage”
It is evident from Figure (c) and (d) that the gradient of the ReLU is zero for negative values of its argument. This can occur for a variety of reasons. For example, consider the case where the input into a neuron is always nonnegative, whereas all the weights have somehow been initialized to negative values. Therefore, the output will be 0. Another example is the case where a high learning rate is used. In such a case, the pre-activation values of the ReLU can jump to a range where the gradient is 0 irrespective of the input. In other words, high learning rates can “knock out” ReLU units. In such cases, the ReLU might not fire for any data instance. Once a neuron reaches this point, the gradient of the loss with respect to the weights just before the ReLU will always be zero. In other words, the weights of this neuron will never be updated further during training.Furthermore, its output will not vary across different choices of inputs and therefore will not play a role in discriminating between different instances. Such a neuron can be considered dead, which is considered a kind of permanent “brain damage” in biological parlance. The problem of dying neurons can be partially ameliorated by using learning rates that are somewhat modest. Another fix is to use the leaky ReLU, which allows the neurons outside the active interval to leak some gradient backwards.
Leaky ReLU
The leaky ReLU is defined using an additional parameter $α ∈ (0, 1)$:
$Φ(v) =α ·v \quad v≤ 0$
$\quad \quad v$ otherwise
Although $α$ is a hyperparameter chosen by the user, it is also possible to learn it. Therefore, at negative values of $v$, the leaky ReLU can still propagate some gradient backwards, albeit at a reduced rate defined by $α < 1$.
The gains with the leaky ReLU are not guaranteed, and therefore this fix is not completely reliable. A key point is that dead neurons are not always a problem, because they represent a kind of pruning to control the precise structure of the neural network. Therefore, a certain level of dropping of neurons can be viewed as a part of the learning process. After all, there are limitations to our ability to tune the number of neurons in each layer. Dying neurons do a part of this tuning for us. Indeed, the intentional pruning of connections is sometimes used as a strategy for regularization. Of course, if a very large fraction of the neurons in the network are dead, that can be a problem as well because much of the neural network will be inactive. Furthermore, it is undesirable for too many neurons to be knocked out during the early training phases, when the model is very poor.
Maxout
A recently proposed solution is the use of maxout networks . The idea in the maxout unit is to have two coefficient vectors $\overline{W_1}$ and $\overline{W_2}$ instead of a single one. Subsequently, the
activation used is $max\{\overline{W_1} ·X,\overline{W_2} ·X\}$. In the event that bias neurons are used, the maxout activation is $max{\overline{W_1} · X + b1,\overline{W_2} · X + b2}$. One can view the maxout as a generalization of the ReLU, because the ReLU is obtained by setting one of the coefficient vectors to 0. Even the leaky ReLU can be shown to be a special case of maxout, in which we set $\overline{W_2} = α\overline{W_1}$ for $α ∈ (0, 1)$. Like the ReLU, the maxout function is piecewise linear. However, it does not saturate at all, and is linear almost everywhere. In spite of its linearity, it has been shown that maxout networks are universal function approximators. Maxout has advantages over the ReLU, and it enhances the performance of ensemble methods like Dropout. The only drawback with the use of maxout is that it doubles the number of required parameters.



Comments
Post a Comment