Mutli Layer Neural Networks, back propagation
Multilayer neural networks contain more than one computational layer. The perceptron contains an input and output layer, of which the output layer is the only computation performing layer. The input layer transmits the data to the output layer, and all computations are completely visible to the user. Multilayer neural networks contain multiple computational layers; the additional intermediate layers (between input and output) are referred to as hidden layers because the computations performed are not visible to the user.
The specific architecture of multilayer neural networks is referred to as feed-forward networks, because successive layers feed into one another in the forward direction from input to output. The default architecture of feed-forward networks assumes that all nodes in one layer are connected to those of the next layer. Therefore, the architecture of the neural network is almost fully defined, once the number of layers and the number/type of nodes in each layer have been defined. The only remaining detail is the loss function that is optimized in the output layer. Although the perceptron algorithm uses the perceptron criterion, this is not the only choice. It is extremely common to use softmax outputs with cross-entropy loss for discrete prediction and linear outputs with squared loss for real-valued prediction.
As in the case of single-layer networks, bias neurons can be used both in the hidden layers and in the output layers. Examples of multilayer networks with or without the bias neurons are shown in Figure (a) and (b), respectively. In each case, the neural network contains three layers. Note that the input layer is often not counted, because it simply transmits the data and no computation is performed in that layer. If a neural network contains $p_1 \ldots p_k$ units in each of its $k$ layers, then the (column) vector representations of these outputs, denoted by $h_1 \ldots h_k$ have dimensionalities $p_1 \ldots p_k$. Therefore, the number of units in each layer is referred to as the dimensionality of that layer.
The weights of the connections between the input layer and the first hidden layer are contained in a matrix $W_1$ with size $d \times p_1$, whereas the weights between the $r$th hidden layer and the ($r + 1$)th hidden layer are denoted by the $p_r × p_{r+1}$ matrix denoted by $W_r$.If the output layer contains $o$ nodes, then the final matrix $W_{k+1}$ is of size $p_k \times o$. The $d$-dimensional input vector $x$ is transformed into the outputs using the following recursive equations:
$\overline{h_1} = \Phi(W_1^T \overline{x}) \qquad [Input to Hidden Layer]$
$\overline{h_{p+1}} = \Phi(W_{p+1}^T \overline{h_p}) \qquad \forall p \in \{1 \ldots k-1 \} \qquad [Hidden to Hidden Layer]$
$\overline{o }= \Phi(W_{k+1}^T \overline{h_{k}}) \qquad [Hidden to Output Layer]$
Here, the activation functions like the sigmoid function are applied in element-wise fashion to their vector arguments. However, some activation functions such as the softmax (which are typically used in the output layers) naturally have vector arguments. Even though each unit of a neural network contains a single variable, many architectural diagrams combine the units in a single layer to create a single vector unit, which is represented as a rectangle rather than a circle. For example, the architectural diagram in Figure (c) (with scalar units) has been transformed to a vector-based neural architecture in Figure (d). Note that the connections between the vector units are now matrices. Furthermore, an implicit assumption in the vector-based neural architecture is that all units in a layer use the same activation function, which is applied in element-wise fashion to that layer. This constraint is usually not a problem, because most neural architectures use the same activation function throughout the computational pipeline, with the only deviation caused by the nature of the output layer.
Note that the aforementioned recurrence equations and vector architectures are valid only for layer-wise feed-forward networks, and cannot always be used for unconventional architectural designs. It is possible to have all types of unconventional designs in which inputs might be incorporated in intermediate layers, or the topology might allow connections between non-consecutive layers. Furthermore, the functions computed at a node may not always be in the form of a combination of a linear function and an activation. It is possible to have all types of arbitrary computational functions at nodes.
Although a very classical type of architecture is shown in Figure above, it is possible to vary on it in many ways, such as allowing multiple output nodes. These choices are often determined by the goals of the application at hand (e.g., classification or dimensionality reduction). A classical example of the dimensionality reduction setting is the autoencoder, which recreates the outputs from the inputs. Therefore, the number of outputs and inputs is equal, as shown in Figure below. The constricted hidden layer in the middle outputs the reduced representation of each instance. As a result of this constriction, there is some loss in the representation, which typically corresponds to the noise in the data. The outputs of the hidden layers correspond to the reduced representation of the data. In fact, a shallow variant of this scheme can be shown to be mathematically equivalent to a well-known dimensionality reduction method known as singular value decomposition. Increasing the depth of the network results in inherently more powerful reductions.
Although a fully connected architecture is able to perform well in many settings, better performance is often achieved by pruning many of the connections or sharing them in an insightful way. Typically, these insights are obtained by using a domain-specific understanding of the data. A classical example of this type of weight pruning and sharing is that of the convolutional neural network architecture , in which the architecture is carefully designed in order to conform to the typical properties of image data. Such an approach minimizes the risk of overfitting by incorporating domain-specific insights (or bias).
Overfitting is a pervasive problem in neural network design, so that the network often performs very well on the training data, but it generalizes poorly to unseen test data. This problem occurs when the number of free parameters, (which is typically equal to the number of weight connections), is too large compared to the size of the training data. In such cases, the large number of parameters memorize the specific nuances of the training data, but fail to recognize the statistically significant patterns for classifying unseen test data. Clearly, increasing the number of nodes in the neural network tends to encourage overfitting. Much recent work has been focused both on the architecture of the neural network as well as on the computations performed within each node in order to minimize overfitting. Furthermore, the way in which the neural network is trained also has an impact on the quality of the final solution. Many clever methods, such as pretraining, have been proposed in recent years in order to improve the quality of the learned solution.
The Multilayer Network as a Computational Graph
It is helpful to view a neural network as a computational graph, which is constructed by piecing together many basic parametric models. Neural networks are fundamentally more powerful than their building blocks because the parameters of these models are learned jointly to create a highly optimized composition function of these models. The common use of the term “perceptron” to refer to the basic unit of a neural network is somewhat misleading, because there are many variations of this basic unit that are leveraged in different settings. In fact, it is far more common to use logistic units (with sigmoid activation) and piecewise/fully linear units as building blocks of these models.
A multilayer network evaluates compositions of functions computed at individual nodes.A path of length 2 in the neural network in which the function $f(·)$ follows $g(·)$ can be considered a composition function $f(g(·))$. Furthermore, if $g1(·), g2(·) . . . gk(·)$ are the functions computed in layer $m$, and a particular layer-$(m+1)$ node computes $f(·)$, then the composition function computed by the layer-$(m + 1)$ node in terms of the layer-$m$ inputs is $f(g1(·), . . . gk(·))$. The use of nonlinear activation functions is the key to increasing the power of multiple layers. If all layers use an identity activation function, then a multilayer network can be shown to simplify to linear regression. It has been shown that a network with a single hidden layer of nonlinear units (with a wide ranging choice of squashing functions like the sigmoid unit) and a single (linear) output layer can compute almost any “reasonable” function. As a result, neural networks are often referred to as universal function approximators, although this theoretical claim is not always easy to translate into practical usefulness.The main issue is that the number of hidden units required to do so is rather large, which increases the number of parameters to be learned. This results in practical problems in training the network with a limited amount of data. In fact, deeper networks are often preferred because they reduce the number of hidden units in each layer as well as the overall number of parameters.
The “building block” description is particularly appropriate for multilayer neural networks.Very often, off-the-shelf softwares for building neural networks2 provide analysts with access to these building blocks. The analyst is able to specify the number and type of units in each layer along with an off-the-shelf or customized loss function. A deep neural network containing tens of layers can often be described in a few hundred lines of code.All the learning of the weights is done automatically by the backpropagation algorithm that uses dynamic programming to work out the complicated parameter update steps of the underlying computational graph. The analyst does not have to spend the time and effort to explicitly work out these steps. This makes the process of trying different types of architectures
relatively painless for the analyst. Building a neural network with many of the off-the-shelf softwares is often compared to a child constructing a toy from building blocks that appropriately fit with one another. Each block is like a unit (or a layer of units) with a particular type of activation. Much of this ease in training neural networks is attributable to the backpropagation algorithm, which shields the analyst from explicitly working out the parameter update steps of what is actually an extremely complicated optimization problem.Working out these steps is often the most difficult part of most machine learning algorithms, and an important contribution of the neural network paradigm is to bring modular thinking into machine learning. In other words, the modularity in neural network design translates to modularity in learning its parameters; the specific name for the latter type of modularity is “backpropagation.” This makes the design of neural networks more of an (experienced) engineer’s task rather than a mathematical exercise.
Training a Neural Network with Backpropagation
In the single-layer neural network, the training process is relatively straightforward because the error (or loss function) can be computed as a direct function of the weights, which allows easy gradient computation. In the case of multi-layer networks, the problem is that the loss is a complicated composition function of the weights in earlier layers. The gradient of a composition function is computed using the backpropagation algorithm.
The backpropagation algorithm leverages the chain rule of differential calculus, which computes the error gradients in terms of summations of local-gradient products over the various paths from a node to the output. Although this summation has an exponential number of components (paths), one can compute it efficiently using dynamic programming. The backpropagation algorithm is a direct application of dynamic programming. It contains two main phases, referred to as the forward and backward phases, respectively. The forward phase is required to compute the output values and the local derivatives at various nodes, and the backward phase is required to accumulate the products of these local values over all paths from the node to the output:
1. Forward phase: In this phase, the inputs for a training instance are fed into the neural network. This results in a forward cascade of computations across the layers, using the current set of weights. The final predicted output can be compared to that of the training instance and the derivative of the loss function with respect to the output is computed. The derivative of this loss now needs to be computed with respect to the weights in all layers in the backwards phase.
2. Backward phase: The main goal of the backward phase is to learn the gradient of the loss function with respect to the different weights by using the chain rule of differential calculus. These gradients are used to update the weights. Since these gradients are learned in the backward direction, starting from the output node, this learning process is referred to as the backward phase.
Consider a sequence of hidden units $h_1, h_2, \ldots, h_k$ followed by output $o$, with respect to which the loss function $L$ is computed.Furthermore, assume that the weight of the connection from hidden unit $h_r $ to $h_{r+1}$ is $w(h_r,h_{r+1})$. Then, in the case that a single path exists from $h_1$ to $o$, one can derive the gradient of the loss function with respect to any of these edge weights using the chain rule:
The aforementioned expression assumes that only a single path from $h_1$ to $o$ exists in the network, whereas an exponential number of paths might exist in reality. A generalized variant of the chain rule, referred to as the multivariable chain rule, computes the gradient in a computational graph, where more than one path might exist. This is achieved by adding the composition along each of the paths from $h_1$ to $o$. An example of the chain rule in a computational graph with two paths is shown in Figure below.Therefore, one generalizes the above expression to the case where a set $P$ of paths exist from $h_r$ to $o$:
The computation of $\frac{\partial h_r}{\partial w_{(h_{r-1},h_r})}$ on the right-hand side is straightforward . However, the path-aggregated term above [annotated by $\bigtriangleup (h_r,o)=\frac{\partial L}{\partial h_r}$] is aggregated over an exponentially increasing number of paths (with respect to path length), which seems to be intractable at first sight. A key point is that the computational graph of a neural network does not have cycles, and it is possible to compute such an aggregation in a principled way in the backwards direction by first computing $ \bigtriangleup(hk, o)$ for nodes $h_k$ closest to $o$, and then recursively computing these values for nodes in earlier layers in terms of the nodes in later layers.Furthermore, the value of $\bigtriangleup(o, o)$ for each output node is initialized as follows:
$\bigtriangleup (o,o)=\frac{\partial L}{\partial o}$
This type of dynamic programming technique is used frequently to efficiently compute all types of path-centric functions in directed acyclic graphs, which would otherwise require an exponential number of operations. The recursion for $\bigtriangleup (h_r,o)$ can be derived using the multivariable chain rule:
Since each $h$ is in a later layer than $h_r, \bigtriangleup (h, o)$ has already been computed while evaluating $\bigtriangleup(hr, o)$. However, we still need to evaluate $\frac{\partial h}{\partial h_r}$ in order to compute the above Equation. Consider a situation in which the edge joining $h_r$ to $h$ has weight $w(h_r,h)$,and let $a_h$ be the value computed in hidden unit $h$ just before applying the activation function $\Phi(·)$. In other words, we have $h = \Phi(a_h)$, where $a_h$ is a linear combination of its inputs from earlier-layer units incident on $h$. Then, by the univariate chain rule, the following expression for $\frac{\partial h}{\partial h_r}$ can be derived:
This value of $\frac{\partial h}{\partial h_r}$ is used in Equation , which is repeated recursively in the backwards direction, starting with the output node. The corresponding updates in the backwards direction are as follows:
Therefore, gradients are successively accumulated in the backwards direction, and each node is processed exactly once in a backwards pass. Note that the computation of Equation
,which requires proportional operations to the number of outgoing edges,needs to be repeated for each incoming edge into the node to compute the gradient with respect to all edge weights.Finally the equation $\frac{\partial h_r}{\partial w_{(h_{r-1},h_r})}$ which is easily computed as
Here, the key gradient that is backpropagated is the derivative with respect to layer activations, and the gradient with respect to the weights is easy to compute for any incident edge on the corresponding unit.
It is noteworthy that the dynamic programming recursion of Equation
can be computed in multiple ways, depending on which variables one uses for intermediate chaining. All these recursions are equivalent in terms of the final result of backpropagation. In the following, we give an alternative version of the dynamic programming recursion, which is more commonly seen in textbooks. Note that Equation
 uses the variables in the hidden layers as the “chain” variables for the dynamic programming recursion. One can also use the pre-activation values of the variables for the chain rule.The pre-activation variables in a neuron are obtained after applying the linear transform (but before applying the activation variables) as the intermediate variables. The pre-activation value of the hidden variable $h = \Phi(a_h)$ is $a_h$.
uses the variables in the hidden layers as the “chain” variables for the dynamic programming recursion. One can also use the pre-activation values of the variables for the chain rule.The pre-activation variables in a neuron are obtained after applying the linear transform (but before applying the activation variables) as the intermediate variables. The pre-activation value of the hidden variable $h = \Phi(a_h)$ is $a_h$. The pre-activation value of the hidden variable $h_r$ is denoted by $a_{hr}$, where:
$h_r =Φ(a_{hr })$
Therefore, instead of above Equation , one can use the following chain rule:
Here, we have introduced the notation $\delta(h_r,o)=\frac{\partial L}{\partial a_{h_r}}$ instead of $\bigtriangleup(h_r,o)=\frac{\partial L}{\partial h_r}$ for setting up the recursive equation. The value of $\delta(o,o)=\frac{\partial L}{\partial a_o}$ is initialized as follows:
Then, one can use the multivariable chain rule to set up a similar recursion:
This recursion condition is found more commonly in textbooks discussing backpropagation. The partial derivative of the loss with respect to the weight is then computed using $\delta(h_r, o)$ as follows:
As with the single-layer network, the process of updating the nodes is repeated to convergence by repeatedly cycling through the training data in epochs. A neural network may sometimes require thousands of epochs through the training data to learn the weights at the different nodes.
One advantage of this recurrence condition over the one obtained using post-activation variables is that the activation gradient is outside the summation, and therefore we can easily compute the specific form of the recurrence for each type of activation function at node hr. Furthermore, since the activation gradient is outside the summation, one can simplify the backpropagation computation by decoupling the effect of the activation function and that of the linear transformation in backpropagation updates.
This simplified approach represents how backpropagation is actually implemented in real systems. From an implementation point of view, decoupling the linear transformation from the activation function is helpful, because the linear portion is a simple matrix multiplication and the activation portion is an elementwise multiplication. Both can be implemented efficiently on all types of matrix-friendly hardware (such as graphics processor units).
The backpropagation process can now be described as follows:
1. Use a forward-pass to compute the values of all hidden units, output $o$, and loss $L$ for a particular input-output pattern $(\overline{X}, y)$.
3.Use the recurrence of Equation $\delta(h_r,o)=\Phi (a_{h_r})\sum_{h:h_r\Rightarrow h} w_{(h_r,h)} \delta(h,o)$ to compute each $δ(h_r, o)$ in the backwards direction.After each such computation, compute the gradients with respect to incident weights as follows:
$\frac{∂L}{∂w(h_{r−1},h{r})}= δ(h_r, o) · h_{r−1}$
The partial derivatives with respect to incident biases can be computed by using the fact that bias neurons are always activated at a value of +1. Therefore, to compute the partial derivative of the loss with respect to the bias of node hr, we simply set $h_{r−1}$ to 1 in the right-hand side of Equation.
4. Use the computed partial derivatives of loss function with respect to weights in order to perform stochastic gradient descent for input-output pattern $(\overline{X}, y)$.
Source: 7-hiddenlayers.com
Updates for Various Activations
One advantage of Equation $\delta(h_r,o)=\Phi (a_{h_r})\sum_{h:h_r\Rightarrow h} w_{(h_r,h)} \delta(h,o)$ is that we can compute the specific types of updates for various nodes. In the following, we provide the instantiation of above Equation for different types of nodes:
$δ(h_r, o) = \sum_{h:h_r\Rightarrow h} w_{(h_r,h)} \delta(h,o)- Linear$ $δ(h_r, o) = h_r(1 − h_r) \sum_{h:h_r\Rightarrow h} w_{(h_r,h)} \delta(h,o)- Sigmoid$
$δ(h_r, o) = (1 − h_r^2) \sum_{h:h_r\Rightarrow h} w_{(h_r,h)} \delta(h,o)- Tanh$
For the ReLU function, the value of $δ(h_r, o)$ can be computed in case-wise fashion:
$δ(h_r, o) = \sum_{h:h_r\Rightarrow h} w_{(h_r,h)} \delta(h,o)$ if $ah_r >0$ and 0 otherwise
A similar recurrence can be shown for the hard tanh function except that the update condition is slightly different:
$δ(h_r, o) = \sum_{h:h_r\Rightarrow h} w_{(h_r,h)} \delta(h,o)$ if $-1<ah_r <1$ and 0 otherwise
The Special Case of Softmax
Softmax activation is a special case because the function is not computed with respect to one input, but with respect to multiple inputs. Therefore, one cannot use exactly the same type of update, as with other activation functions.
The softmax converts $k $real-valued predictions $v_1 . . . v_k$ into output probabilities $o_1 . . . o_k$ using the following relationship:
$o_i =\frac{exp(v_i)}{\sum_{j=1}^k exp(v_j)}\qquad ∀i ∈ {1, . . . , k}$
Note that if we try to use the chain rule to backpropagate the derivative of the loss $L$ with respect to $v_1 . . . v_k$, then one has to compute each $\frac{∂L}{∂o_i}$ and also each $\frac{∂o_i}{∂v_j}$.
This backpropagation of the softmax is greatly simplified, when we take two facts into account:
1. The softmax is almost always used in the output layer.
2. The softmax is almost always paired with the cross-entropy loss. Let $y_1 . . . y_k ∈ {0, 1}$ be the one-hot encoded (observed) outputs for the $k$ mutually exclusive classes. Then, the cross-entropy loss is defined as follows:
$L = −\sum_{i=1}^k y_ilog(o_i)$
The key point is that the value of $\frac{∂L}{∂v_i}$ has a particularly simple form in the case of the
softmax:
$\frac{∂L}{∂v_i}=\sum_{j=1}^k \frac{∂L}{∂o_j}. \frac{∂o_j}{∂v_i}= o_i − y_i$
Therefore, in the case of the softmax, one first backpropagates the gradient from the output to the layer containing $v_1 . . . v_k$. Further backpropagation can proceed according to the rules discussed earlier in this section








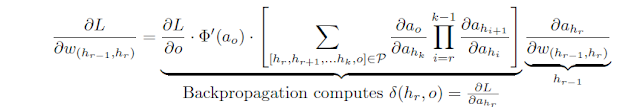






Comments
Post a Comment